肖特基二极管中磁场超快产生的技术研究

  图1(a)表示本实验中所用的结。它由n型GaAs(001)基片在超高真空中生长12层单分子层Co₂₅Fe₇₅薄膜组成。沉积30层单分子金箔帽，以防止样品在进行实验时受外界压力的腐蚀。静态克尔测量表明，当沿易磁化轴[110]方向加场，在平面取向内矫顽场 ~24Oe呈二次滞后。在器件底部作欧姆接触，在顶部金属层和GaAs基底之间可加电压。为两种不同的目的使用锁模钛宝石激光器输出的超短光脉冲&(约150fs)：1)作抽运，将约800mm波长的激光脉冲聚焦成直径约2µm的斑点(每个脉冲的能量为 0.5~1.5mJ/cm²)。这束光产生把磁化矢量偏离平衡态所需的磁场脉冲(后面我们详细说明)；2)作探测， 脉冲光束倍频后通过相同的保偏物镜定向(光斑尺寸约1µm，每个脉冲能量约 0.75mJ/cm²)
  利用反向光偏振的变化，通过磁极结构中的磁光克尔效应探测磁化强度的垂直分量。用各种滤光片阻止反射的抽运光束进入探测器。为探测方便，抽运束由机械斩波成1.6kHz，用在乌拉斯顿棱镜后面两个光电二极管组成的电桥，用锁相技术测量信号。为避免光学元件和样品过热，没有用足约76MHz激光重复率，用最高工作频率约4.76MHz的脉冲采样器降低脉冲重复率。通过改变抽运脉冲和探测脉冲之间的时间延迟!可以皮秒精度测量磁化矢量垂直分量的时间演变。此外，可以把抽运脉冲相对于探测脉冲调偏约1µm使得抽运脉冲可以在探测脉冲周围的小圆圈内定位[图1(a)]。

  图1 实验装置和磁场的对称性。(a)用重复率4.76MHz脉冲持续时间150fs的激光脉冲序列作实验时标。抽运束和探测束都用100倍物镜(数值孔径0.95)馈入，聚焦到Au/Fe/GaAs(001)结构中，抽运束斑点可以在围绕探测束的圆周上移动;(b)在样品平面中产生的脉冲磁场H的对称性以及等价磁场Meq的指向。在抽运束参考坐标中，测量了A~E位置。结果表明，磁场振幅与相对于抽运束的位置有关。当偏压Us=0时，估计最大磁场强度约25Oe
 
  假设抽运脉冲通过结，垂直于膜平面发射电流!则磁力线应是在结平面中的圆，其中心在抽运脉冲的位置[图1(b)] 薄膜磁化沿易磁化轴[110]方向[图1(b)]中的箭头在相同平面内，因此，沿圆周，平衡磁化矢量和脉冲磁场矢量之间的所有角度都实现。在磁场平行于或反向平行于磁化强度的位置，M×H=0，   
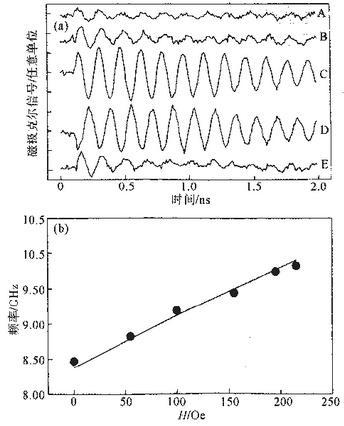
  没有扭矩作用于平衡磁化矢量，且不产生激发[图1(b)]中的A和B位置](由于两束或剩余垂直磁场分量之间有轻微的不准直,存在一些剩余磁激发)。相反，在磁化强度垂直于所加磁场脉冲的位置，扭矩为最大，激发出与平衡构型的偏离最大，导致类铁磁共振(FMR)图1(b)
的C和D位置]。如果抽运束和探测束调准在样品上的相同点，则仅观测到很小的磁化强度振荡，因为磁场强度被抵消或降低[图1(b)中E的位置]。在图1(b)右边是磁场剖面图，它是抽运束和探测束相对位置的函数，计算是用安培定律插入测量的光斑尺寸，并假设为高斯电流剖面进行的。下面讨论场强。
  图1所示的器件产生的磁场确实可以在器件的磁性激活一边引起进动运动。图2(a)给出了振荡的垂直分量作为抽运脉冲和探测脉冲之间时间延迟函数的曲线，对应图1(b)中的五种不同区域(A、B、C、D、E)。正如预期的那样，最大的振荡分量在最大扭矩区(C和D)。注意C和D曲线的一个重要细节；它们的相位差π，这个相移反映在C和D区域扭矩的符号相反。进一步证明，图2(a)中的曲线描述铁磁薄膜中的进动运动，它是通过测量在C点[图2(b)]振荡频率与沿易磁化轴的静磁场H的关系提供的。静态克尔磁测量法分析表明，存在很大的单轴各向异性(各向异性磁场H_u=570±80 Oe)。忽略由于四次分量H₁=13±5 Oe对各向异性能量微小贡献可以使用铁磁共振频率的Kittel表达式拟合这些数据： Ma是饱和磁化强度。图2(b)中通过数据点的连续线是用Kittel方程当(4πM_R)_off=15kOe(用超导量子干涉装置磁测量法确定的)，γ=-γeg/2(γe是电子的回磁比，g为朗道因子)时得到的。作为一贯性检查，从拟合确定出CoFe合金的g因子为-2.0，对铁磁组分Fe和Co，这个值似乎合理。本质上，在图2(b)中施加磁场条件下，进动频率值与单轴磁各向异性和形状各向异性所给出的内部场描述的值一致。需要指出，抽运束强度减小三倍，进动频率不变。可
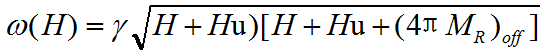
以得出结论，激发的垂直分量足够小，证明用Kittel方程是合理的，并且在进运时间尺度内抽运束没有改变铁磁体的磁学特性。
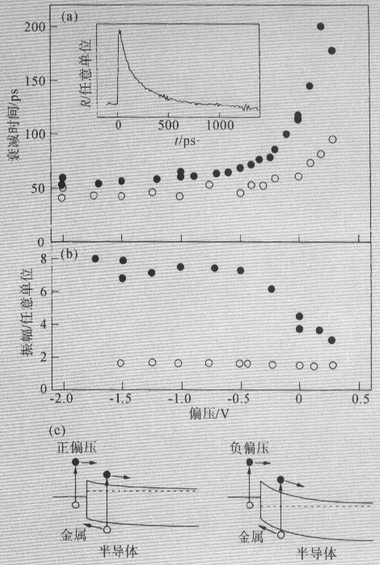
  图2中的实验结果表明，在肖特基结上局部电流注入产生颇大的超快磁场。现在来估计磁场强度，引起光电流的关键机理是抽运激光激发出电子-空穴对，在肖特基位垒耗尽区的电场将电子-空穴对分开，空穴被注入铁磁体、电子扫进半导体，于是便产生了电流对瞬态电流脉冲第二种贡献是从铁磁体向半导体发射电子。第二种贡献和空穴注入同样重要，但目前实验不能区分它们，以激光脉冲感生的外电荷改变反射率R：测量R随时间的变化，可作为外电荷的时间演变[图3(a)插图]。可以看到，由于载流子的产生，R(t)突然增加，然后按指数R(t)=R_0e^-t/t缓慢衰减。因为电流I(t)等于单位时间流过的电让我们可以从衰减的反射率信号估计瞬态电流：I(t)∝1/τe^-t/t。每个脉冲产生的载流子总数(由宏观光电导电流决定，在目前情况，在零偏压时为-20mA)导致磁场在几皮秒内上升到峰值，用安培定律可以保守地估计，在零偏压和以时间常数τ衰减时大约是25Oe。当偏压Us从0降至≤1.5V，相应振荡振幅倍增时，以1/τ为标尺的最大场，粗略估计其强度倍增。这个估计与图3(b)中数据一致[在确定振荡振幅时，我们用朗道-利弗尼兹方程估计指数因子的作用，发现在感兴趣的瞬时范围(60-200ps)，振幅仅与前因子有关，这正是我们所说的以1/τ为标尺的最大场]。注意，进动运动的线性排除了磁化强度反转，没有反转是不奇怪的，因为进动反转所需的场是各向异性场。
  通过改变跨接在肖特基位垒上的电压就可调谐磁场。图3(a)表示衰减时间τ与跨接位垒电压的关系。这是由于在肖特基位垒内分离了产生载流子，减小了内在的电场，延迟了过扫描时间。在低抽运功率(-0.5mJ/cm²)时，可以忽略空间电荷效应，预期过扫描由内在场决定，且过扫描时间与所加电压关系不大。确实，τ几乎与施加电压无关[见图3(a)圈]。相反，在高抽运功率(1.5mJ/cm²)时，空间电荷效应很强，导致对Us≥-0.5V的耗散区总电场强烈减少，结果τ与所加电压强烈相关[图3(a)，点]。
  τ与电压的相关性产生了电流与电压的相关性，通过测量类铁磁共振振荡振幅与Us的关系，观测到这种关系[见图3(b)，在图1(b)中C的位置]。其中还考虑了高抽运水平(点)1.5mJ/cm²和抽运水平降低约3倍的情况(圈，0.5mJ/cm²)。在图3(b)中有两个电压区一个是Us≤-0.6V的反偏压区，这时振幅几乎是常数，并且振幅值近似与抽运功率成线性关系。在这个区域，整个系统由肖特基位垒形成，磁膜以线性方式工作。另一个区域(Us≥-0.6V)，在高抽运功率时，振幅随Us增加而减小，直到Us≈0.4V(没有施加更高电压，以避免高直流电流损坏二极
管)。对低抽运功率，振幅没有明显变化，当Us≥-0.5V时，高抽运功率和低抽运功率的曲线彼此靠近。注意，当Us改变符号时，振荡既不改变符号，也不消失，显然，我们所处理的肖特基结，甚至当正电压时，能带仍然在耗散区弯曲[见图3(c)]。在高抽运功率时，振荡振幅下降与载流子过扫描时间的增加相对应。在载流子数目为常数时，随着增加载流子过扫描时间，最大磁场强度减小，并且正如观察到的，振荡振幅也减小。对低抽运功率，在我们的实验中，仅观测到振幅非常微弱地减小，这与过扫描时间适度增加是相符的。   图3 二极管电压特性。(a)在插图内给出样品反射率R作为抽运脉冲和探測脉冲之间时间延迟的函数。时间延迟用指数关系R=R^oe-t/t拟合。在低抽运动率(圈)和高抽运功率(点)时，将扫描输出时间τ作为偏压的函数作图；(b)在施加磁场为零时，类铁磁共振的振幅与施加在结上的直流偏压的关系。注意在高抽运强度(点)和低抽运强度(圈)时有不同的振幅；(c)对正偏压和负低压在金属-半导体结处能带弯曲。在两种情况下，带上升的方向都是朝向金属一边
 
  我们可以得出结论，肖特基二极管可以作为与电压有关的“磁场抽运”方式工作。此研究最直接应用是在显示进动动力学的实验场所产生超快磁场。由于高度集成化，避免了以超快方式产生磁场必须从远处源带来磁元件的全部常规结构。从源向磁元件传输电流脉冲，用匹配不当的电子学波导反射时，磁场脉冲没有畸变，因为它是由磁元件本身产生的。由于最大感应磁场与光斑尺寸相关，所以减小光斑尺寸，或用侧向花样为纳米直径的混合式结，可能产生足够强的场激发进动开关。



上一篇：肖特基二极管整流效率计算与测量方式
下一篇：SiC肖特基二极管的反向特性技术